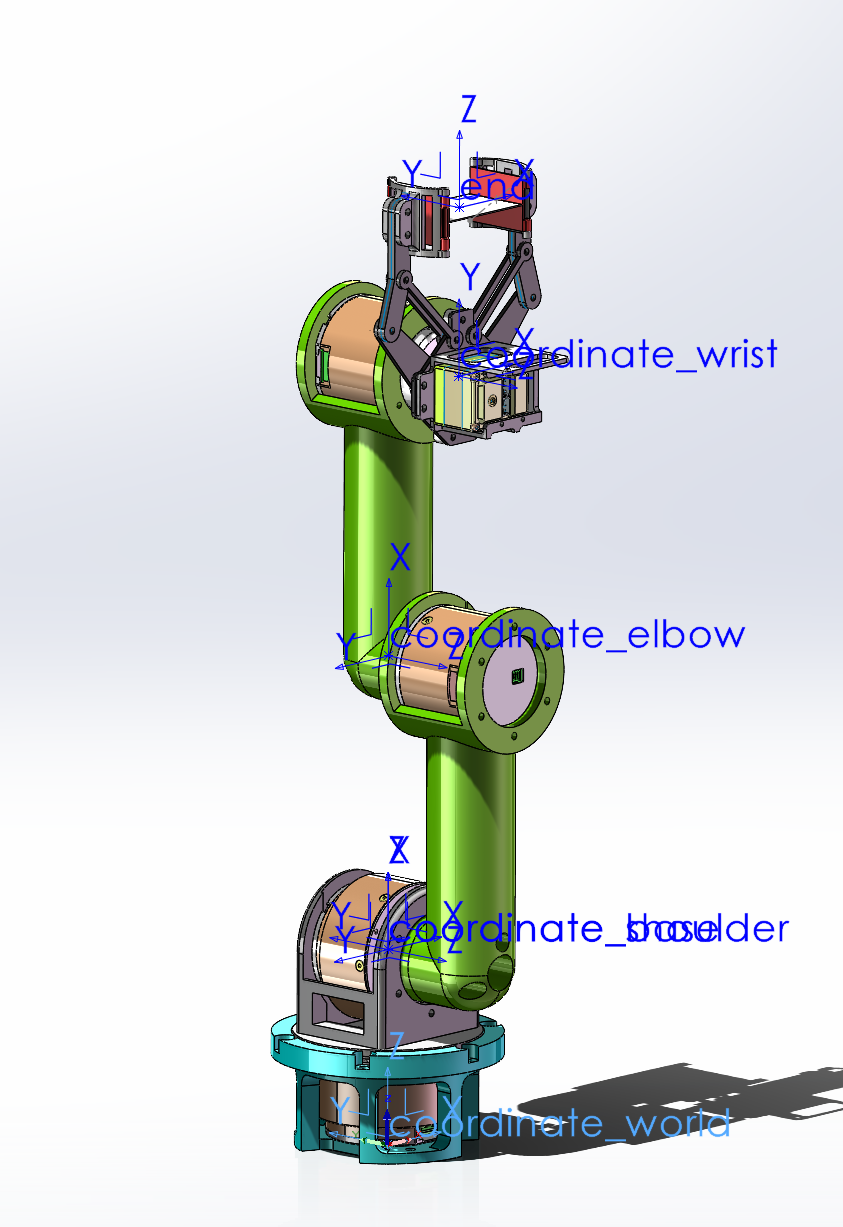
♪³ 机械臂机械模型
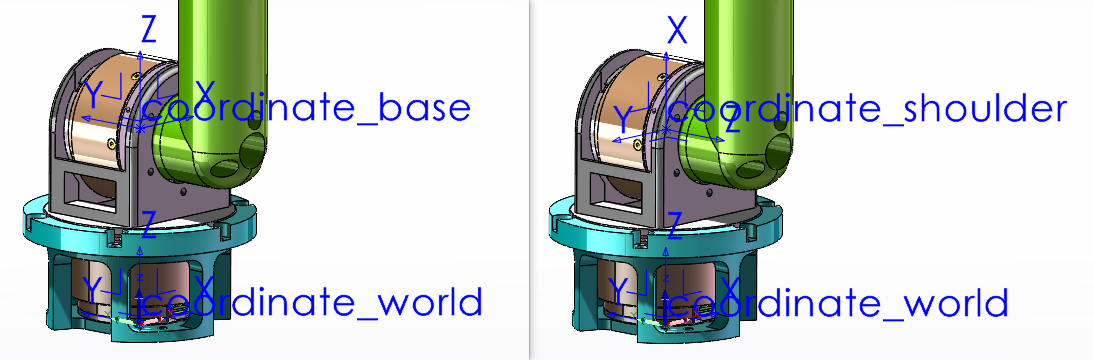
这里,我为了运动学建模的方便,让基座(base)坐标系和肩部(shoulder)坐标系原点重合,他们只有旋转方向不同,但 Z Z Z
关节:
base:绕竖直轴,旋转;
shoulder:绕水平轴1,旋转;
elbow:绕水平轴2,旋转;
wrist:绕水平轴3,旋转;
end:移动关节;
♪³ MDH正运动学建模
MDH法:
MDH四个参数含义如下:
a i a_i a i α i \alpha_i α i d i d_i d i θ i \theta_i θ i
MDH参数:
i = i= i = 关节类型 α i − 1 \alpha_{i-1} α i − 1 a i − 1 a_{i-1} a i − 1 d i d_i d i θ i \theta_i θ i 关节变量 1 R 0 0 0 0 0 0 0.08525 0.08525 0.08525 q 1 q_1 q 1 q 1 q_1 q 1 2 R π / 2 \pi /2 π /2 0 0 0 0 0 0 q 2 + π / 2 q_2+\pi /2 q 2 + π /2 q 2 q_2 q 2 3 R 0 0 0 0.12893 0.12893 0.12893 0 0 0 q 3 q_3 q 3 q 3 q_3 q 3 4 R 0 0 0 0.129 0.129 0.129 0.04039 0.04039 0.04039 q 4 − π / 2 q_4-\pi /2 q 4 − π /2 q 4 q_4 q 4 5 P − π / 2 -\pi /2 − π /2 0 0 0 d 5 + 0.07403 d_5+0.07403 d 5 + 0.07403 0 d 5 d_5 d 5
之后根据DH参数表和单节变换矩阵公式,把每一个变换矩阵求出来
MDH 通用单节矩阵:(i = 1 , 2 , 3 , 4 , 5 i=1,2,3,4,5 i = 1 , 2 , 3 , 4 , 5
A i = T i i − 1 = [ cos θ i − sin θ i cos α i − 1 sin θ i sin α i − 1 a i − 1 cos θ i sin θ i cos θ i cos α i − 1 − cos θ i sin α i − 1 a i − 1 sin θ i 0 sin α i − 1 cos α i − 1 d i 0 0 0 1 ] A_i = T_i^{i-1} =
\begin{bmatrix}
\cos\theta_i & -\sin\theta_i\cos\alpha_{i-1} & \sin\theta_i\sin\alpha_{i-1} & a_{i-1}\cos\theta_i \\
\sin\theta_i & \cos\theta_i\cos\alpha_{i-1} & -\cos\theta_i\sin\alpha_{i-1} & a_{i-1}\sin\theta_i \\
0 & \sin\alpha_{i-1} & \cos\alpha_{i-1} & d_i \\
0 & 0 & 0 & 1
\end{bmatrix} A i = T i i − 1 = cos θ i sin θ i 0 0 − sin θ i cos α i − 1 cos θ i cos α i − 1 sin α i − 1 0 sin θ i sin α i − 1 − cos θ i sin α i − 1 cos α i − 1 0 a i − 1 cos θ i a i − 1 sin θ i d i 1 这里角标可以这样理解:p 0 p^0 p 0 o 1 0 o_1^0 o 1 0 o 1 o_1 o 1 0 0 0 1 1 1 0 0 0 0 0 0 1 1 1 0 0 0 R 1 0 R^0_1 R 1 0 1 1 1 0 0 0 1 1 1 0 0 0
于是从世界坐标系 O 0 O_0 O 0 O 1 O_1 O 1 α 0 = 0 , a 0 = 0 , d 1 = 0.08525 , θ 1 = q 1 \alpha_0=0,\ a_0=0,\ d_1=0.08525,\ \theta_1=q_1 α 0 = 0 , a 0 = 0 , d 1 = 0.08525 , θ 1 = q 1
T 1 0 = [ cos q 1 − sin q 1 0 0 sin q 1 cos q 1 0 0 0 0 1 d 1 0 0 0 1 ] T_1^{0} =
\begin{bmatrix}
\cos q_1 & -\sin q_1 & 0 & 0 \\
\sin q_1 & \cos q_1 & 0 & 0 \\
0 & 0 & 1 & d_1 \\
0 & 0 & 0 & 1
\end{bmatrix} T 1 0 = cos q 1 sin q 1 0 0 − sin q 1 cos q 1 0 0 0 0 1 0 0 0 d 1 1 从基座坐标系 O 1 O_1 O 1 O 2 O_2 O 2 α 1 = π 2 , a 1 = 0 , d 2 = 0 , θ 2 = q 2 + π 2 \alpha_1=\frac{\pi}{2},\ a_1=0,\ d_2=0,\ \theta_2=q_2+\frac{\pi}{2} α 1 = 2 π , a 1 = 0 , d 2 = 0 , θ 2 = q 2 + 2 π
T 2 1 = [ − sin q 2 0 cos q 2 0 cos q 2 0 sin q 2 0 0 1 0 0 0 0 0 1 ] T_2^{1} =
\begin{bmatrix}
-\sin q_2 & 0 & \cos q_2 & 0 \\
\cos q_2 & 0 & \sin q_2 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix} T 2 1 = − sin q 2 cos q 2 0 0 0 0 1 0 cos q 2 sin q 2 0 0 0 0 0 1 从肩部坐标系 O 2 O_2 O 2 O 3 O_3 O 3 α 2 = 0 , a 2 = 0.12893 , d 3 = 0 , θ 3 = q 3 \alpha_2=0,\ a_2=0.12893,\ d_3=0,\ \theta_3=q_3 α 2 = 0 , a 2 = 0.12893 , d 3 = 0 , θ 3 = q 3
T 3 2 = [ cos q 3 − sin q 3 0 a 2 cos q 3 sin q 3 cos q 3 0 a 2 sin q 3 0 0 1 0 0 0 0 1 ] T_3^{2} =
\begin{bmatrix}
\cos q_3 & -\sin q_3 & 0 & a_2\cos q_3 \\
\sin q_3 & \cos q_3 & 0 & a_2\sin q_3 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix} T 3 2 = cos q 3 sin q 3 0 0 − sin q 3 cos q 3 0 0 0 0 1 0 a 2 cos q 3 a 2 sin q 3 0 1 从肘部坐标系 O 3 O_3 O 3 O 4 O_4 O 4 α 3 = 0 , a 3 = 0.129 , d 4 = 0.04039 , θ 4 = q 4 − π 2 \alpha_3=0,\ a_3=0.129,\ d_4=0.04039,\ \theta_4=q_4-\frac{\pi}{2} α 3 = 0 , a 3 = 0.129 , d 4 = 0.04039 , θ 4 = q 4 − 2 π
T 4 3 = [ sin q 4 cos q 4 0 a 3 sin q 4 − cos q 4 sin q 4 0 − a 3 cos q 4 0 0 1 d 4 0 0 0 1 ] T_4^{3} =
\begin{bmatrix}
\sin q_4 & \cos q_4 & 0 & a_3 \sin q_4 \\
-\cos q_4 & \sin q_4 & 0 &-a_3 \cos q_4 \\
0 & 0 & 1 & d_4 \\
0 & 0 & 0 & 1
\end{bmatrix} T 4 3 = sin q 4 − cos q 4 0 0 cos q 4 sin q 4 0 0 0 0 1 0 a 3 sin q 4 − a 3 cos q 4 d 4 1 从腕部坐标系 O 4 O_4 O 4 O 5 O_5 O 5 α 4 = − π 2 , a 4 = 0 , d 5 = q 5 + 0.07403 , θ 5 = 0 \alpha_4=-\frac{\pi}{2},\ a_4=0,\ d_5=q_5+0.07403,\ \theta_5=0 α 4 = − 2 π , a 4 = 0 , d 5 = q 5 + 0.07403 , θ 5 = 0
cos θ 5 = 1 , sin θ 5 = 0 , cos α 4 = 0 , sin α 4 = − 1 \cos\theta_5=1,\ \sin\theta_5=0,\ \cos\alpha_4=0,\ \sin\alpha_4=-1 cos θ 5 = 1 , sin θ 5 = 0 , cos α 4 = 0 , sin α 4 = − 1
T 5 4 = [ 1 0 0 0 0 0 1 0 0 − 1 0 d 5 0 0 0 1 ] T_5^{4} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 &-1 & 0 & d_5 \\
0 & 0 & 0 & 1
\end{bmatrix} T 5 4 = 1 0 0 0 0 0 − 1 0 0 1 0 0 0 0 d 5 1 最终总的正运动学就是:T 5 0 = T 1 0 T 2 1 T 3 2 T 4 3 T 5 4 T_5^{0} = T_1^{0}\ T_2^{1}\ T_3^{2}\ T_4^{3}\ T_5^{4} T 5 0 = T 1 0 T 2 1 T 3 2 T 4 3 T 5 4 p 5 p_5 p 5 p 0 p_0 p 0 p 0 = T 5 0 p 5 p_0=T_5^0 \ p_5 p 0 = T 5 0 p 5
为了方便书写,这里做一些变量定义:
s 12 = sin ( q 1 + q 2 ) , c 12 = cos ( q 1 + q 2 ) , s 34 = sin ( q 3 + q 4 ) , c 34 = cos ( q 3 + q 4 ) . \begin{aligned}
&s_{12} = \sin(q_1+q_2),\quad c_{12} = \cos(q_1+q_2),\\
&s_{34} = \sin(q_3+q_4),\quad c_{34} = \cos(q_3+q_4).
\end{aligned} s 12 = sin ( q 1 + q 2 ) , c 12 = cos ( q 1 + q 2 ) , s 34 = sin ( q 3 + q 4 ) , c 34 = cos ( q 3 + q 4 ) . 将齐次变换矩阵写为:
T 5 0 ( q ) = [ R ( q ) p ( q ) 0 0 0 1 ] T_5^{0}(q) =
\begin{bmatrix}
R(q) & p(q) \\
0\ 0\ 0 & 1
\end{bmatrix} T 5 0 ( q ) = [ R ( q ) 0 0 0 p ( q ) 1 ] 其中姿态部分,即旋转矩阵 R ( q ) R(q) R ( q )
R ( q ) = [ s 12 s 34 − c 12 − s 12 c 34 s 34 c 12 − s 12 c 12 c 34 c 34 0 s 34 ] R(q)=
\begin{bmatrix}
s_{12}s_{34} & -c_{12} & - s_{12}c_{34}\\
s_{34}c_{12} & -s_{12} & c_{12}c_{34}\\
c_{34} & 0 & s_{34}
\end{bmatrix} R ( q ) = s 12 s 34 s 34 c 12 c 34 − c 12 − s 12 0 − s 12 c 34 c 12 c 34 s 34 位置部分 p ( q ) = [ x , y , z ] T p(q)=[x,y,z]^T p ( q ) = [ x , y , z ] T
x = − a 2 s 12 cos q 3 − a 3 s 12 s 34 + ( d 4 + q 5 + d 5 o f f s e t ) c 12 , y = − a 2 c 12 cos q 3 + a 3 c 12 s 34 + ( d 4 + q 5 + d 5 o f f s e t ) s 12 , z = a 2 sin q 3 − a 3 c 34 + d 1 \begin{aligned}
x &= -a_2s_{12}\cos q_3\ - a_3s_{12}s_{34} + (d_4 + q_5 + d_{5offset})c_{12},\\[4pt]
y &= \phantom{-}a_2 c_{12}\cos q_3\ + a_3 c_{12} s_{34} + (d_4 + q_5 + d_{5offset}) s_{12},\\[4pt]
z &= a_2 \sin q_3\ - a_3 c_{34} + d_1
\end{aligned} x y z = − a 2 s 12 cos q 3 − a 3 s 12 s 34 + ( d 4 + q 5 + d 5 o ff se t ) c 12 , = − a 2 c 12 cos q 3 + a 3 c 12 s 34 + ( d 4 + q 5 + d 5 o ff se t ) s 12 , = a 2 sin q 3 − a 3 c 34 + d 1 最终的齐次变换矩阵为:
T 5 0 ( q ) = [ s 12 s 34 − c 12 − s 12 c 34 x s 34 c 12 − s 12 c 12 c 34 y c 34 0 s 34 z 0 0 0 1 ] T_5^{0}(q)=
\begin{bmatrix}
s_{12} s_{34} & -c_{12} & - s_{12} c_{34} & x \\
s_{34} c_{12} & -s_{12} & c_{12} c_{34} & y \\
c_{34} & 0 & s_{34} & z \\
0 & 0 & 0 & 1
\end{bmatrix} T 5 0 ( q ) = s 12 s 34 s 34 c 12 c 34 0 − c 12 − s 12 0 0 − s 12 c 34 c 12 c 34 s 34 0 x y z 1 ♪³ Python机器人工具箱验证
这里不用Matlab进行验证,Matlab的RTB工具箱环境有点配置不来...,同样的代码,我在这台电脑能正确建模,另一台就不行了,因此改用Python版本的RTB工具箱
可以按照以下步骤配置好Python环境,这里需要注意的是,numpy和matplotlib版本都不能过高
bash
复制 1 conda create -n "robotics" python=3.9
2 pip install "numpy<2"
3 pip install "matplotlib<3.8"
4 pip install roboticstoolbox-python spatialmath-python swift-sim
5
RTB中自带有MDH的建模函数,实际上工程上都是也用MDH,下面直接填入DH参数,调用MDH进行正运动学建模:
python
复制 1 import numpy as np
2 import roboticstoolbox as rtb
3 from roboticstoolbox.robot.DHLink import RevoluteMDH, PrismaticMDH
4 from roboticstoolbox import DHRobot
5
6 # theta1 = q1
7 # theta2 = q2 + pi/2
8 # theta3 = q3
9 # theta4 = q4 - pi/2
10 L1 = RevoluteMDH(d=0.08525, a=0.0, alpha=0.0, offset=0.0)
11 L2 = RevoluteMDH(d=0.0, a=0.0, alpha=np.pi/2, offset=np.pi/2)
12 L3 = RevoluteMDH(d=0.0, a=0.12893, alpha=0.0, offset=0.0)
13 L4 = RevoluteMDH(d=0.04039, a=0.129, alpha=0.0, offset=-np.pi/2)
14 L5 = PrismaticMDH(theta=0.0,a=0.0, alpha=-np.pi/2,offset=0.07403, qlim=[0.0, 0.04])
15
16 myarm = DHRobot([L1, L2, L3, L4, L5], name="My5DOF")
17
18
19 if __name__ == "__main__":
20 print(myarm) # 打印 DH 表
21 print("=== 正运动学测试 ===")
22
23 q_home = np.array([0, 0, 0, 0, 0]) # [q1,q2,q3,q4,d5]
24 q_home_deg = np.degrees(q_home)
25 T_home = myarm.fkine(q_home) # 末端 SE3 变换
26 T_home_mat = T_home.A
27 T_pose = (T_home_mat[0:3, 3][0], T_home_mat[0:3, 3][1], T_home_mat[0:3, 3][2])
28 T_home_euler_deg = T_home.rpy(order='zyx', unit='deg') # 提取欧拉角部分,ZYX 顺序
29 T_home_euler_rad = T_home.rpy(order='zyx', unit='rad')
30 x, y, z = T_pose
31 roll, pitch, yaw = T_home_euler_rad
32 pos_home = np.array([x, y, z, roll, pitch, yaw])
33 print("零位置: ")
34 print(f"关节空间坐标(rad): {np.round(q_home, 4)}")
35 print(f"关节空间坐标(deg): {np.round(q_home_deg, 4)}")
36 print(f"工作空间坐标: {np.round(pos_home, 4)}")
37
38 # 随便给一组关节量再算一次
39 q_test_deg = np.array([0, -30.6, -42.6, 37.5, 0.02])
40 q_test = np.array([np.radians(0), np.radians(-30.6),
41 np.radians(-42.6), np.radians(37.5), 0.02])
42 T_test = myarm.fkine(q_test)
43 T_test_mat = T_test.A
44 T_test_pose = (T_test_mat[0:3, 3][0], T_test_mat[0:3, 3][1], T_test_mat[0:3, 3][2])
45 T_test_euler_deg = T_test.rpy(order='zyx', unit='deg')
46 T_test_euler_rad = T_test.rpy(order='zyx', unit='rad')
47 x, y, z = T_test_pose
48 roll, pitch, yaw = T_test_euler_rad
49 pos_test = np.array([x, y, z, roll, pitch, yaw])
50 print("测试位姿: ")
51 print(f"关节空间坐标(rad): {np.round(q_test, 4)}")
52 print(f"关节空间坐标(deg): {np.round(q_test_deg, 4)}")
53 print(f"工作空间坐标: {np.round(pos_test, 4)}")
54
55 # 调用 teach,可以启动带滑块的示教器
56 # 初始姿态用 q_home
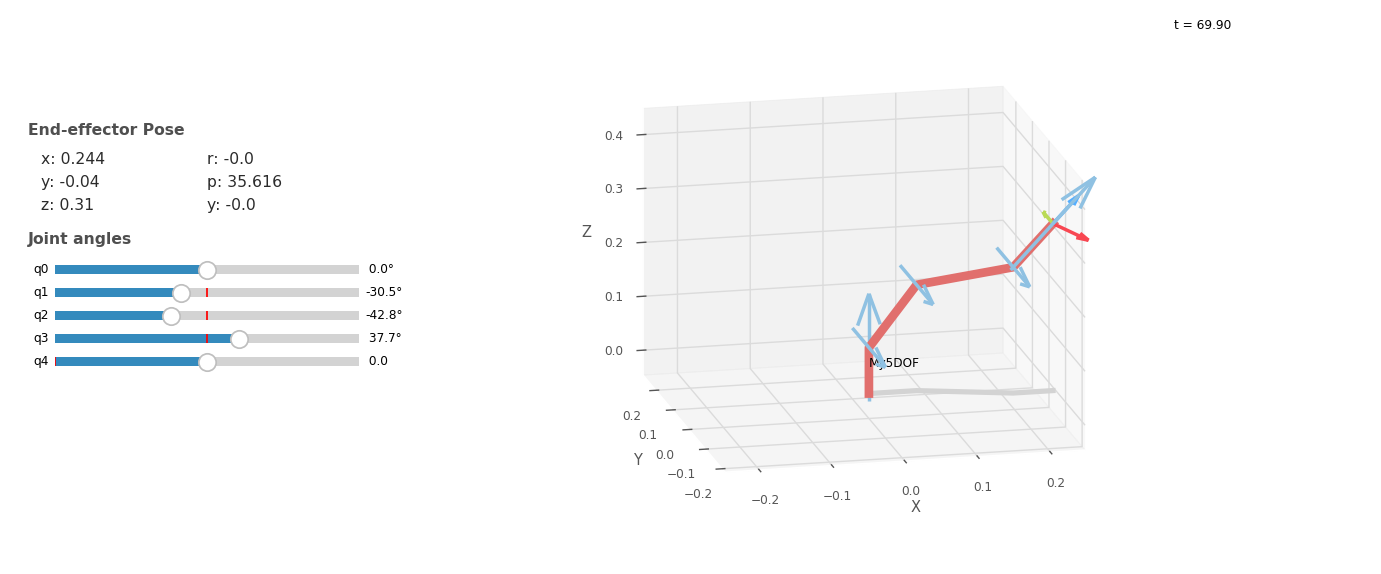
57 myarm.teach(q_home)
58
结果如下:
bash
复制 1 ...
2 === 正运动学测试 ===
3 零位置:
4 关节空间坐标(rad): [0 0 0 0 0]
5 关节空间坐标(deg): [0. 0. 0. 0. 0.]
6 工作空间坐标: [ 0. -0.0404 0.4172 0. -0. 0. ]
7 测试位姿:
8 关节空间坐标(rad): [ 0. -0.5341 -0.7435 0.6545 0.02 ]
9 关节空间坐标(deg): [ 0.00e+00 -3.06e+01 -4.26e+01 3.75e+01 2.00e-02]
10 工作空间坐标: [ 0.244 -0.0404 0.3099 -0. 0.6231 -0. ]
11