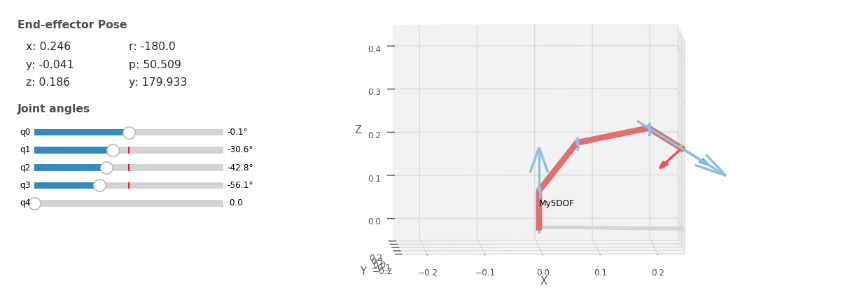
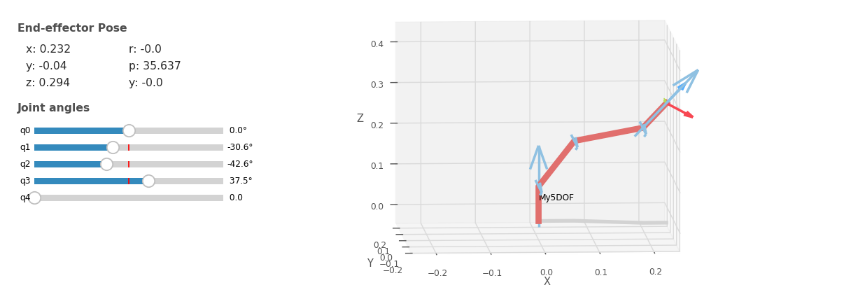
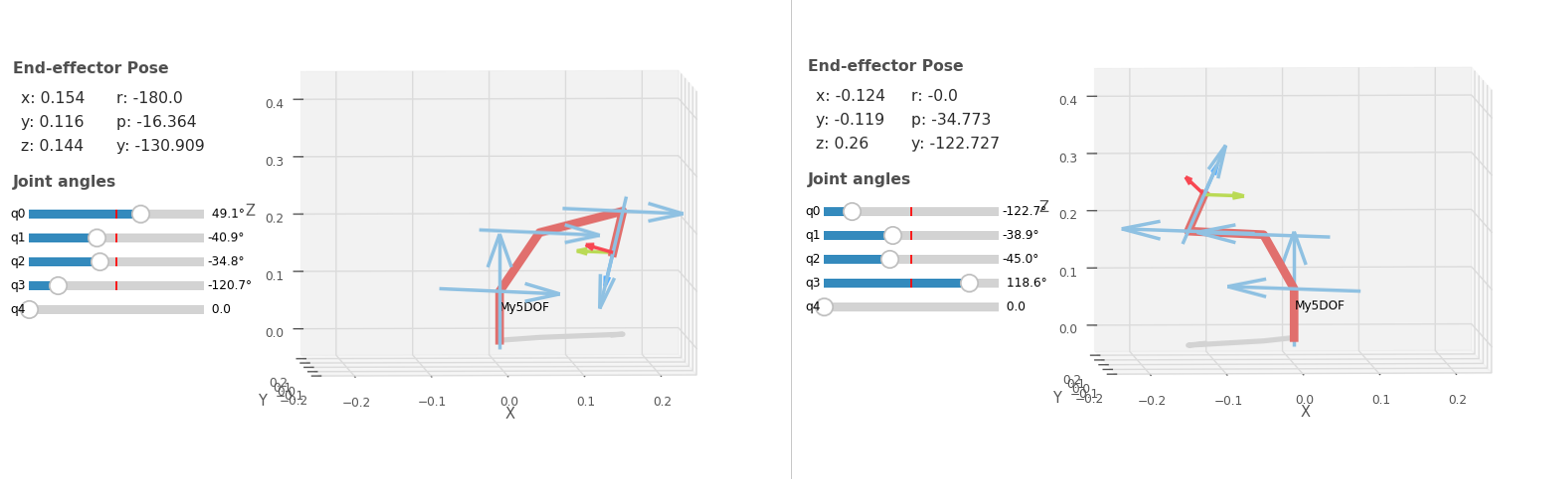
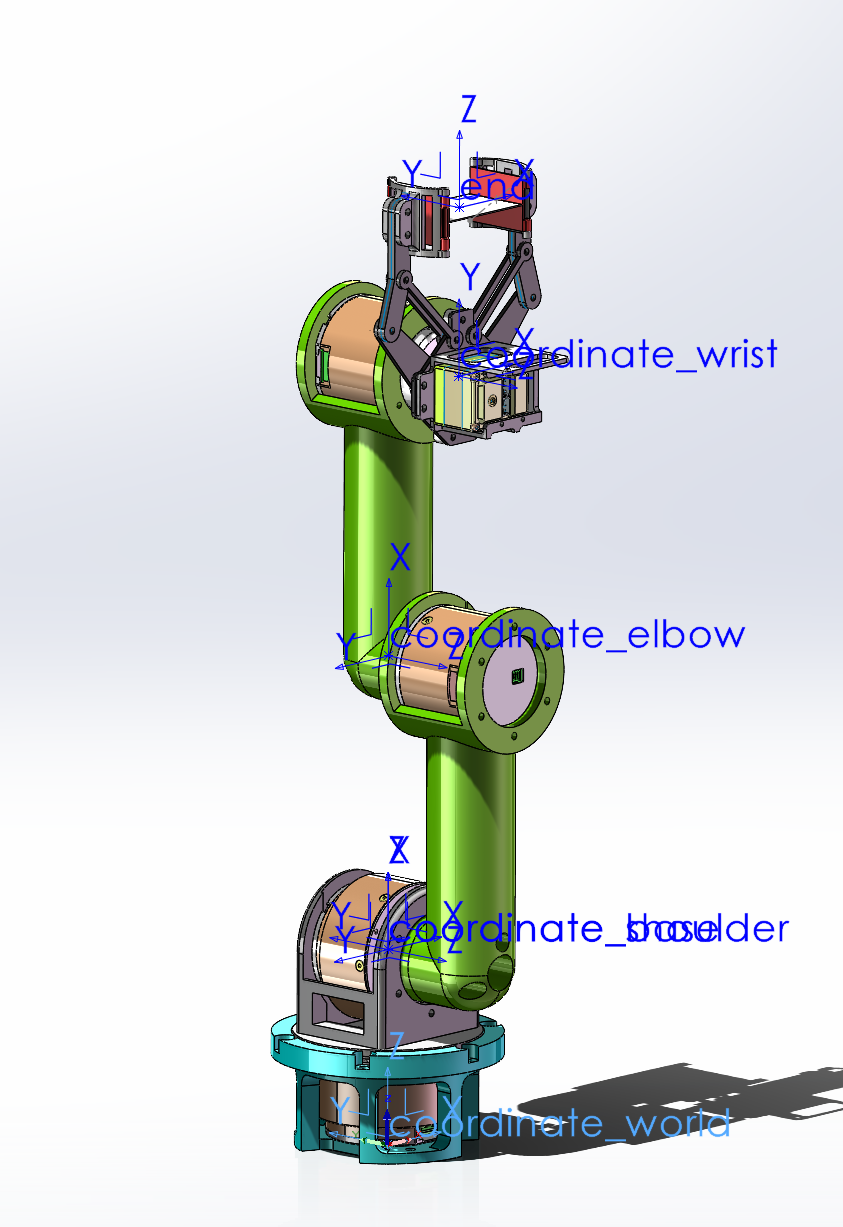
♪³ 机械臂模型图
MDH表
| 关节类型 | 关节变量 | |||||
|---|---|---|---|---|---|---|
| 1 | R | |||||
| 2 | R | |||||
| 3 | R | |||||
| 4 | R | |||||
| 5 | P | 0 |
这个机械臂实际上来自于本科时参加一个科技竞赛时和队友一同自主设计搭建的小车上的机械臂,由4个旋转关节和1个移动关节构成,比赛时的任务就是抓物料和码垛物料,因此它是码垛机器人的变体
整个机械臂共 5 个自由度,无法到达空间中任意的位置和姿态 (6D Pose),因此末端位姿可以看作是:
- 末端位置
- 末端俯仰角 ;
即少了 这个欧拉角;
通常 类型的欧拉角包含:,在这个机械臂中, 值只能取 或 ,从正运动学时的示教器可以看出这一点
♪³ 运动学逆解-解析法
第5个关节是一个夹爪,看作棱柱关节,先不参与求解;
于是问题分为两部分:平面定位 和平面内构型
运动学参数:
- 基座高度:
- 手腕侧向偏移:
- 大臂长度:
- 小臂长度:
- 夹爪末端伸长:
求解
1.求解基座关节 ;
关节1负责调整机械臂的朝向,由于存在侧向偏移 ,机械臂去够某个点 的时候,存在一个偏置角度,设末端在基坐标系下的位置为 ,则水平距离为 ,
由于 的存在,末端手腕的平面不过原点,而是与基座平分面平行,且与原点距离为 的平面;
基座的旋转有下面两种情况:
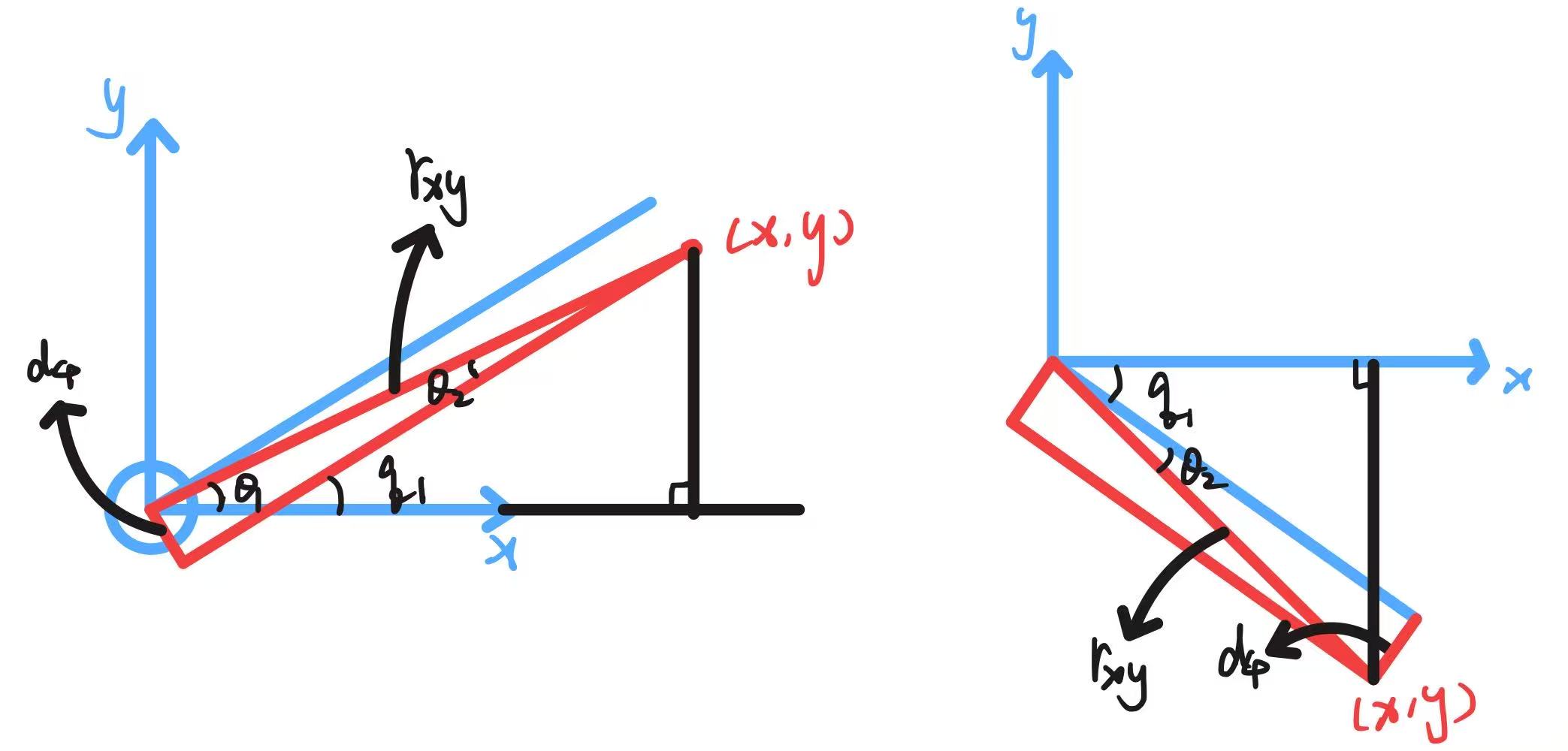
不论是哪一种,都满足(取右手的情况):
此处应该注意,需满足 否则末端位置无法到达;
2.投影到手臂平面(基座平分面)
将末端坐标 ,转换到由 构成的竖直平面内,才能方便计算 ,在该竖直平面内的,末端的坐标为 :
其中,
为径向距离,即末端投影到水平面后,沿着手臂到基座中心的距离,由于 是垂直于平面的,平面内的有效伸展距离为:
为 关节坐标系中心相对于地面的高度:
3.求解平面关节
之后, 就变成了平面的三连杆问题,定义俯仰角 (末端相对于水平面的夹角),末端执行器 的位置是由 的中心加上长度 沿着 方向延伸得到,且 ,因此 正方向的方向向量在这个竖直平面内,且方向由 决定,因此俯仰角
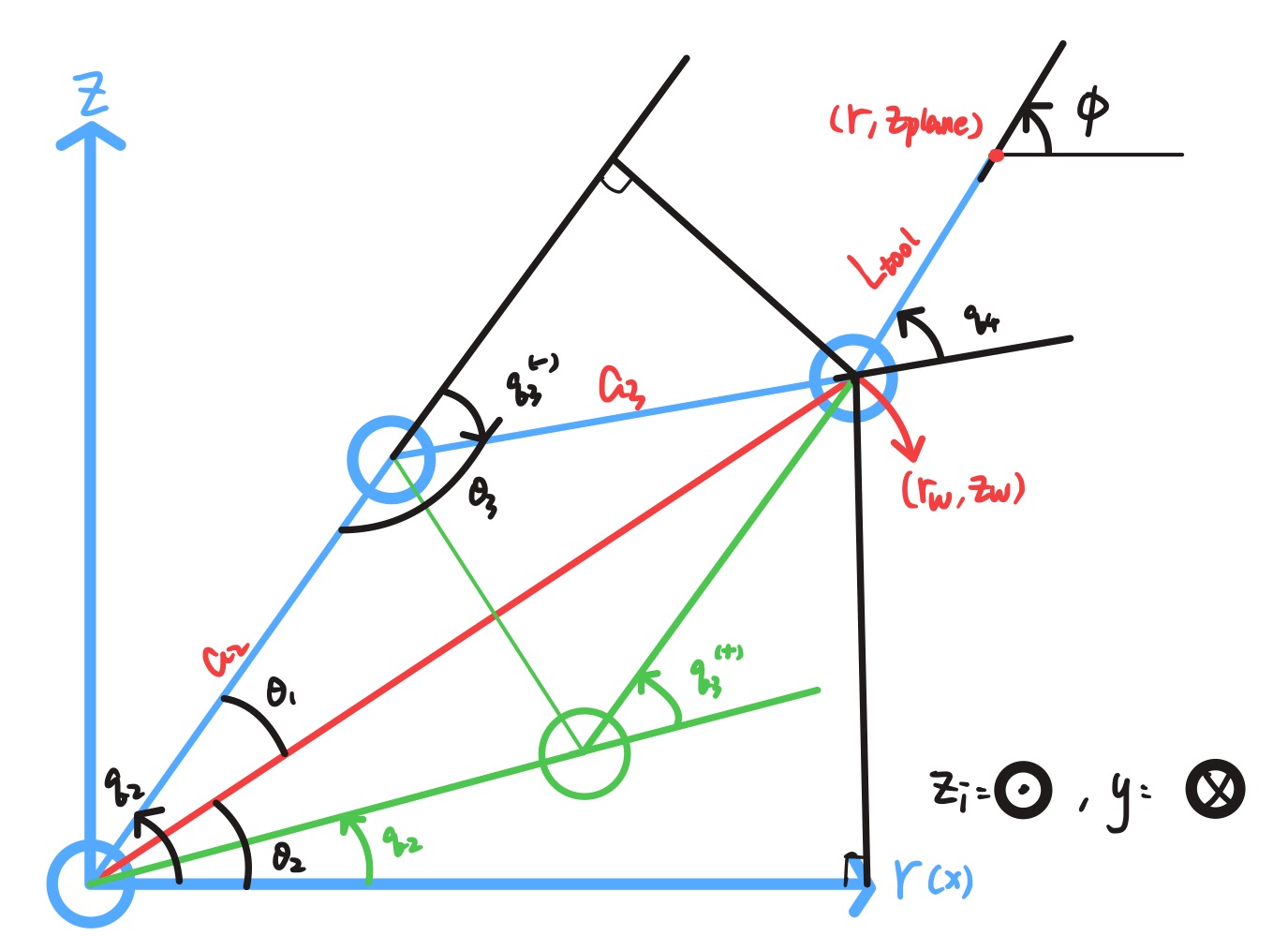
平面三连杆存在二解,通常取肘部上凸的构型(即图中蓝色部分)
先将工具末端平面坐标 转换到手腕中心在平面内的坐标 :
之后通过几何法求解 (两杆逆解,类似余弦定理):
则有:
其中:
继续求 :
最后求解 ,由于总的俯仰角 是所有关节角的累加(需要考虑 offset),关节 的 ,关节 的 ,于是最终全局角度关系为:
因此可得:
这里的 是末端连杆相对于水平面的绝对角度,和欧拉角中的 不完全等价,需要进行一定的变换,具体可参考后文的代码部分,此外由于肩部关节在定义的时候存在一个 的正偏置,在关节空间中 的时候在上文的解析运算的值是 ,因此在返回 时需减去 的偏置值,这一点也可以参考后文的代码,而 的偏置无需处理,因为求解出来的角度零轴刚好沿着机械臂展延伸方向
最终完整实现了从末端工作空间坐标 到关节空间坐标 的转换( 视为已知,因为机械臂末端是一个舵机控制的夹爪,方便起见认为只有开和闭两种状态,两种状态下对应的长度已知)
♪³ 仿真验证
对于 类型的欧拉角
此机械臂 roll = 0 或 -pi,pitch 为-90°~90°
roll = 0 时,说明头朝上,phi = 90° - pitch
roll = -pi时,说明头朝下,phi = pitch - 90°
逆运动学的Python仿真代码如下:
python
经过验证,下面四种情况能能正确地从工作空间坐标变换回关节变量,此外,为了使机械臂都保持这种肘部上凸构型,对关节变量 的范围进行了限制:(示教器中未计入偏置值,因此示教器中的范围是 ),